I doubt I need to list for you the many titles of the 18th century German savant and polymath Johann Wolfgang von Goethe, but allow me to add one or two that were new to me, at least: color theorist (or phenomenologist of color) and progenitor of abstract expressionism. As a fascinating Booktryst post informs us, Goethe’s book on color, Zur Farbenlehre (Theory of Colors), written in 1810, disputed the Newtonian view of the subject and formulated a psychological and philosophical account of the way we actually experience color as a phenomenon. In his account, Goethe describes how he came by his views:
Along with the rest of the world I was convinced that all the colors are contained in the light; no one had ever told me anything different, and I had never found the least cause to doubt it, because I had no further interest in the subject.
But how I was astonished, as I looked at a white wall through the prism, that it stayed white! That only where it came upon some darkened area, it showed some color, then at last, around the window sill all the colors shone… It didn’t take long before I knew here was something significant about color to be brought forth, and I spoke as through an instinct out loud, that the Newtonian teachings were false.
Schopenhauer would later write that “[Goethe] delivered in full measure what was promised by the title of his excellent work: data toward a theory of colour. They are important, complete, and significant data, rich material for a future theory of colour.” It was a theory, Schopenhauer admits, that does not “[furnish] us with a real explanation of the essential nature of colour, but really postulates it as a phenomenon, and merely tells us how it originates, not what it is.”
Another later philosophical interpreter of Goethe, Ludwig Wittgenstein—a thinker greatly interested in visual perception—also saw Goethe’s work as operating very differently than Newton’s optics—not as a scientific theory but rather as an intuitive schema. Wittgenstein remarked that Goethe’s work “is really not a theory at all. Nothing can be predicted by means of it. It is, rather, a vague schematic outline, of the sort we find in [William] James’s psychology. There is no experimentum crucis for Goethe’s theory of colour.”
Yet a third later German genius, Werner Heisenberg, commented on the influence of Zur Farbenlehre, writing that “Goethe’s colour theory has in many ways borne fruit in art, physiology and aesthetics. But victory, and hence influence on the research of the following century, has been Newton’s.”
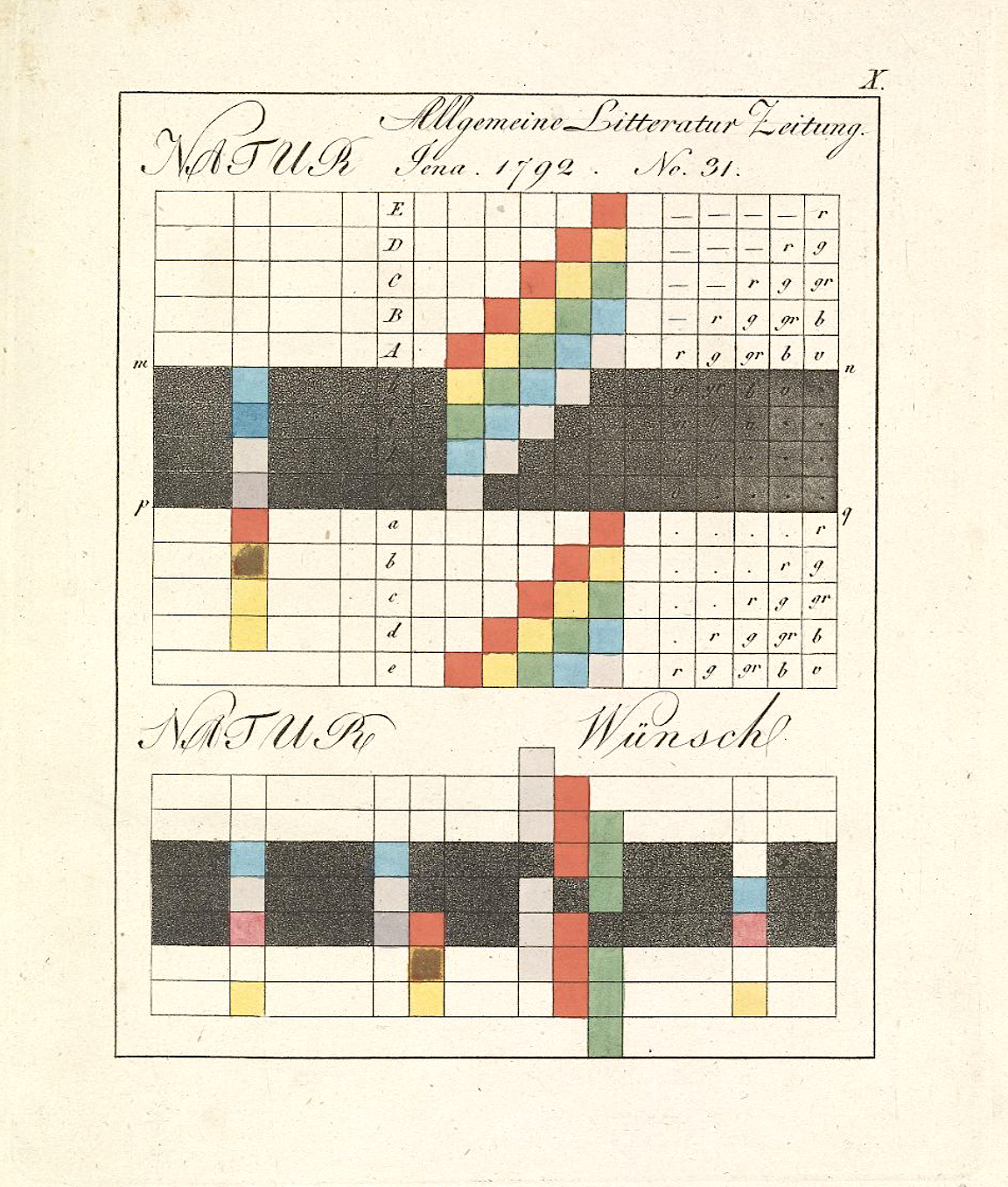
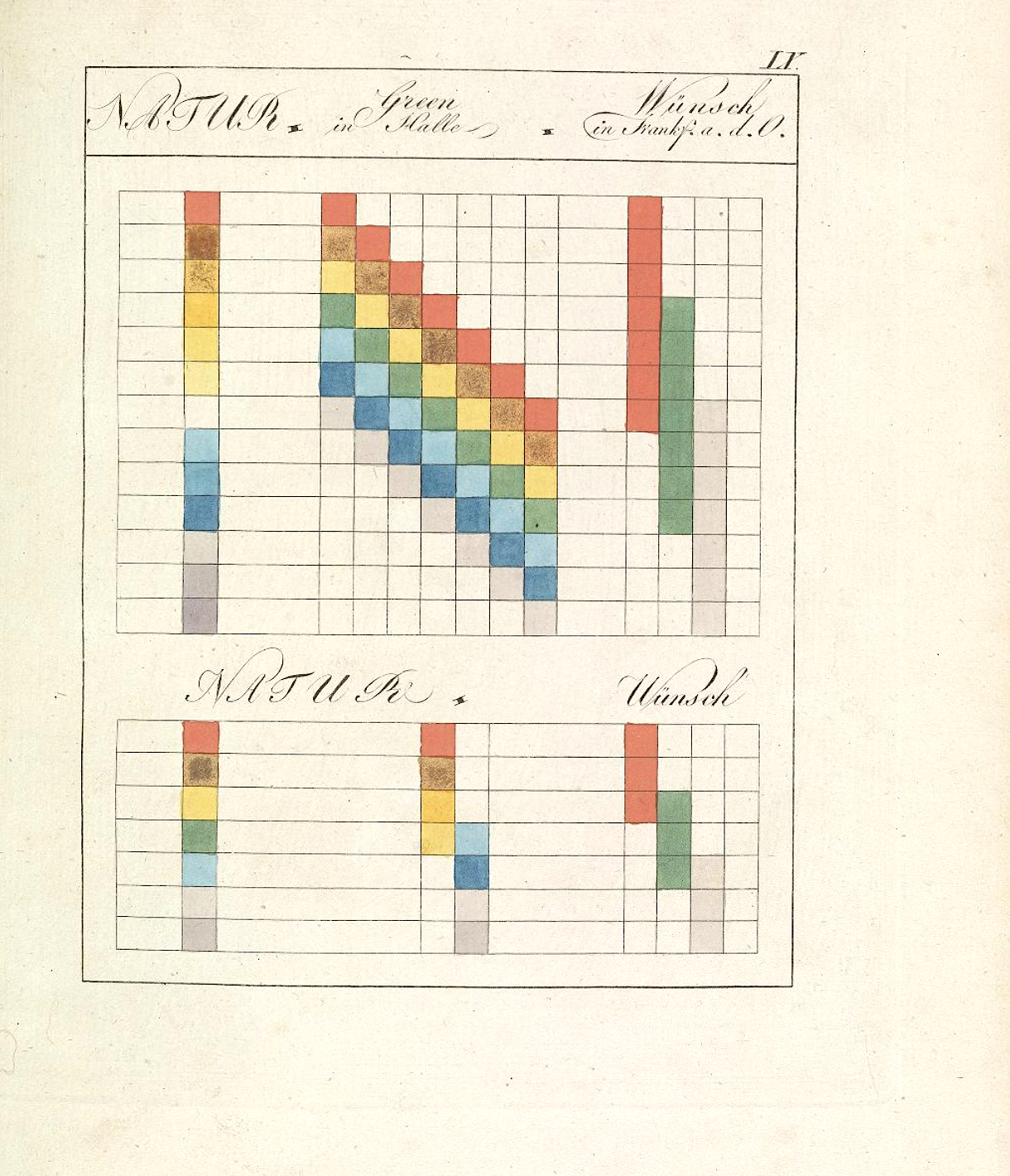
I’m not fit to evaluate the relative merits of Goethe’s theory, or lack thereof, versus Newton’s rigorous work on optics. Whole books have been written on the subject. But whatever his intentions, Goethe’s work has been well-received as a psychologically accurate account that has also, through his text and many illustrations you see here, had significant influence on twentieth century painters also greatly concerned with the psychology of color, most notably Wassily Kandinsky, who produced his own “schematic outline” of the psychological effects of color titled Concerning the Spiritual in Art, a classic of modernist aesthetic theory. As is usually the case with Goethe, the influence of this single work is wider and deeper than he probably ever foresaw.
You can find Goethe’s Theory of Colors in our collection of 700 Free Ebooks. It’s also available in audio format in our collection of Free Audio Books. An affordable version can also be purchased on Amazon.
Related Content:
The Tale of the Fox: Watch Ladislas Starevich’s Animation of Goethe’s Great German Folktale (1937)
Wassily Kandinsky Caught in the Act of Creation, 1926
When Respected Authors, from Goethe to Henry Miller, Try Their Hand at Painting
Josh Jones is a writer and musician based in Durham, NC. Follow him at @jdmagness
Modern Color theorist S.H.Rogoff discovered the double or reverse after-image 1952 displayed on the cover of J.Albers first ‘Color Interaction. Hal as Albers graduate assistant task with putting the booklet had 3-4ths of his own color modules included in the booklet. Among many of concepts of Hal’s Color theory thesis titled ‘Optical Illusions and Vibrational Theory’ denoted his correction of erroneous nature of the concept called Simultaneous Contrast to redefine Simultaneous Presence. A great example of this early work is on a FB page https://www.facebook.com/media/set/?set=a.586991144659431.1073741829.586980831327129&type=1
A review of a book about color in movies.
https://cen.acs.org/articles/84/i7/Movie-Symbolism-Amazing-Technicolor.html
Thanks; never heard of Goethe’s color work
You can find Goethe’s book on colour here: http://theoryofcolor.org/Theory+of+Color
Thanks for the great little article.
Isaac Newton’s Scam Spectrum – Several ways to make it observable and how they disprove his colour theory
R.S.W.Bobbette 2018
The repeatedly observable fact is that colours generated in and through prisms never originate from a “rainbow spectrum”, but always from pairs of variably separated bands of colours related to relative dark-light contrasts. These bands are about equal in overall width, with the central stripe of each less distinct than the outer two. Initially, no green colour occurs nor any spectrum. The appearance of a “rainbow spectrum” is a secondary effect, a parlour trick that can be accomplished in several instructive ways.
The first method is the one used by Newton to put over his farcical, but mathematically accessible, idea of colour production. Of course, the method of the scam in this case is to reduce the body of white light to where the otherwise and actually separate colour bands slightly overlap or intersect. This is the basic principle of all forms of the scam. This first method allows a portable result, the narrow beam of light, to avoid the embarrassing drawing together of the two pre-existing colour bands, where the colours actually originate. The fact that the colour bands arise separated by variable distances (i.e. refractive angles) means that the blue colour is not the “other half” of the same light that is behind the red band. This is only implied by the scam spectrum. The scam spectrum also hides, or makes hard to discriminate, that the purple and violet stripes of the blue colour band are actually projected or illuminated in front of relative darkness, from the side; the complete red colour band is clearly seen to be shone through from behind. These three facts do not readily suggest a uniform approach along any lines put forward by Newton, etc.
The “rainbow spectrum” is not created by one unified beam of light being split into colours, but from two diametrically opposite, separate beams of already coloured light being brought together by reducing what separates them to where they combine to create the otherwise non-existent green colour. An equally applied “differential refraction” is not an option.
This first example has the light going through the prism and the colours being observed on a surface. It is also possible to create the scam by observing the colour bands directly through the prism. If you look at a bright window, through a prism, you will notice the colour bands on either side of the window, along the line of refraction. Now we can see the reason for a concept like refraction, when we twist the prism back and forth and see the dramatic narrowing and broadening of the light image of the window. This measurable phenomenon is the basis of refraction, and therefore of differential refraction, and it is this that allows us to produce a second version of Newton’s Scam Spectrum. If you twist the prism far enough, you reduce the light of the window to where – voila! – you have the “rainbow spectrum”, down the line of refraction.
But there are some problems here. No matter how you broaden or shrink the window image, the colour bands remain unaltered to any visible extent. This at least suggests that they occur after the light is bent. They merely move and follow the light-dark contrast line. When brought together, both bands move towards the narrow angle of the prism, but the red one moves much more quickly and “catches up” with the blue. They remain unaltered until reaching the scam spectrum, when they begin to overlap or intersect, with the yellow and blue stripes changing to green, until they merge and are replaced by one green stripe. Only now do the colour bands begin to shrink, but not equally. Orange and purple disappear first, with red, green and violet disappearing together as the light is choked off.
Furthermore, the colour bands have the ability to move in two different directions, or at different speeds, within themselves. Let me explain. There is a small shelf edge projecting into the window view, and this shows the identical red band as the side of the window, but much shorter and projected about one and a half band widths into the window. Now as you tilt the prism to shrink the window, this shelf projection shrinks in accord with refraction, until about three colour band widths from the blue band, it disappears into the overall edge. But throughout this entire span, the small colour band has been following the shrinking shelf, moving backwards into the main edge colour band while the whole moves forward. No “differential refraction” can accommodate these appearances, disappearances and movements.
Prisms certainly should be accorded much more honest, interested study. Another way of producing Newton’s Scam Spectrum requires a bit of set-up but is, I think, worth the interesting results.
Take flat black and flat white paint, mix equally to paint grey a pole 2 inches wide and 5 feet high. Paint a piece of cardboard 2×5 feet flat black and a piece 2×3 feet flat white (it’s relative dimensions and not actual measurements that matter). Stand the grey pole in front of the black board in bright light, and look at it through the prism. You will see the clearest “rainbow spectrum” down the line of the pole. There are two ways of showing this to be a version of Newton’s Scam Spectrum. To do the first you put the white board over the lower half of the black, and look; suddenly at the white border the blue band turns to red and the red to blue, continuing down the line of refraction. So we have the remarkable anachronism of Newton’s Scam Spectrum cheek to jowl with a “complete” inverted spectrum, with red meeting violet in the middle! Placing the white just to the right or the left of the pole produces a “complete spectrum” of either two red or two blue bands…
The creation of colour in a prism is repeatedly seen to be more closely related to relative dark-light contrasts than to either refraction or any necessary red – blue continuum. This change of colour from blue to red down the line of refraction, merely because the background changes from relatively dark to relatively light, shows up as lies all the concepts of prismatic colour production put forward by Newton and his idolizers. The fact that the blue band abuts the red one on the same line of refraction is also absolute proof that, far from being parts of a rightfully belonging together “rainbow spectrum”, the colour bands are indirectly related to each other at best. This shows the absurdity (if previous evidence hasn’t) of there being any possibility of refraction, differential or otherwise, in the production of these phenomena of colour. The only certain relationship to refraction is the left-right orientation of the bands, and probably their width.
The trick to Newton’s Scam Spectrum in this case is the narrowness of the pole. Staple a sheet of writing paper to the pole and you will see the colour bands separated.
Finally, and less explicitly, by twisting around a prism in sizeable bright light, the “rainbow spectrum” can be seen projected onto surfaces, represented by at least three examples. One duplicates the window method, with a bright spot that is reduced by twisting the prism until the bands meet. Another has the bright spot visible on a card near the prism, but reducing in size until 8-10 feet away (in this example) a “spectrum” appears. The third traces back to the ninety degree angles of the prism, but shows no bright spot. It is aligned with the bands on either side of the angle and is certainly a projective version of the narrow pole effect.
These are the few methods I have been able to attempt; I’m sure there are others. Again, every supposed colour spectrum arising from a prism can be resolved into the actually existing separate colour bands. These arise in prisms at opposite sides of the body of light, adjacent to relative darkness. The light involved in the red side of the scam spectrum is not involved in the creation of the blue side.
PostScript…
It should be noted that the “inverted spectrum” compresses to produce a magenta stripe that replaces the red and violet ones, as the otherwise non-existent green replaces the blue and yellow. Any physics of prismatic colour relationships, that is not fantasy, will have to address four initially occurring colours, plus four derived from their combining. The prismatic “seven colours of the rainbow spectrum”, with everything derived from it, have been made up for mathematical convenience and easy salesmanship, and do not represent soundly reported investigative science.
Newton’s Scam Spectrum – Prismatic Colour Observed
R.S.W.Bobbette 2020
ABSTRACT
Through prisms, there is no continuously variable ‘spectrum’ spontaneously produced; all continuous patterns of colour occur due to structurally narrow or spatially manipulated proximity of the actually spontaneous edge- or contrast- effect light/dark interactions that produce two actually separate colour bands. The fact that prismatic colours reverse depending on whether the light/dark interaction is directly perceived or seen reflected proves that these colours are not produced by the prism directly, but by the relative perspective context of the light/dark relationship… including both a bright body in a dark ground or a dark body in a bright ground. It is this light/dark interaction that leaves the prism, with brightness bent in front of darkness giving violet on the dark side, indigo at the light/dark edge, and blue on the bright side. Red occurs with brightness seen behind bent darkness on the dark side, orange at the light/dark edge, and yellow on the bright side. This relationship holds in both visual contexts –e.g., directly perceived the darkness is clearly seen through the brightness to give violet, while on the same side the brightness will strike the reflective surface first and be seen through the following darkness to give red. Prismatic green is an artifact of the bright body narrowed to produce the intersection of the two bright side colours – blue and yellow. Mauve is similarly produced by reducing the dark body to integrate the dark side colours red and violet. Physicists have ignored any thorough description of the actual occurrence of colour through prisms, as it in no way supports their mathematically convenient fantasy of the nature of colour.
CONTENTS
NEWTON’S SCAM SPECTRUM……………………..1
HONEST OBSERVATION ………………………………7
PRISMATIC COLOUR ……………………………………9
THE TWO VISUAL CONTEXTS……………………….14
Similarities …………………………………………………14
Differences ………………………………………………..15
LIMITS…………………………………………………………16
“…the reason of the colours arising on the edges is much the same, as will appear to one that shall a little consider it.” Well, let’s see what “…will appear to one that shall a little consider it.”
NEWTON’S SCAM SPECTRUM
Physicists, without question, believe Isaac Newton’s claim that the production of a rainbow-like row of colours from a narrow light beam through a prism, which he dubbed a spectrum, is a spontaneous, continuously variable event and proves that the light splits into colours; which if true could only be due to the individual colours reacting differently to the resistance to transmission shown by the bending of the light (differential refraction). But, the repeatedly observable fact is that colours generated in and through prisms never spontaneously originate from a ‘rainbow spectrum’, but always from pairs of bands of three colours adjacent to or across relative dark-light contrasts, opposite to each other and separated by variable and moveable distances. These bands, called here the ‘red band’ and ‘blue band’ are about equal in overall width, with the central colour stripe of each less distinct than the outer two. To begin with, no green colour occurs nor any spectrum.
As a caution to those eager to proclaim illusory, merely physiological colours, it should be noted that all colour phenomena described here can be recorded digitally through a CMOS sensor exactly on a par with ‘real’ colours. And those who rush to bring in phenomena from other contexts of colour generation and manipulation, should remember that whales were studied as fish for centuries – pertinence must be proven by other than this or that similarity.
What is presented here is only intended to be considered in the context of prisms. The appearance of a ‘rainbow spectrum’ through a prism is a secondary effect, a parlour trick that can be accomplished in several instructive ways.
The first method is the one used by Newton to put over his mathematically convenient, but scientifically inadequate, idea of colour production. Of course, the method of the scam in this case is to reduce the body of white light to where the otherwise and actually separate colour bands slightly overlap or intersect. This is the basic principle of all forms of the scam. This first method allows a portable result, the narrow beam of light, to avoid the embarrassing drawing together of the two pre-existing colour bands, where the colours actually spontaneously originate. The fact that these colour bands arise and maintain their form separated by variable and moveable distances (i.e. differing refractive angles) means that the blue band is not produced by the ‘other half’ of the same light that is behind the red band. This is only incompetently claimed as proven by the artificially formed scam spectrum. The scam spectrum also hides, or makes hard to discriminate, the fact that the green stripe is merely the result of the bringing together of the spontaneous blue and the yellow stripes, and that it actually replaces these if the bands are compressed further. These two facts do not readily suggest a uniform explanation that is “much the same” as the mathematics put forward by Newton, or any other refraction theory. The ‘rainbow spectrum’ is not created by one unified beam of light being split into colours, but from two diametrically opposite, separate beams of already coloured light being brought together by reducing what separates them to where they combine to create the otherwise non-existent green colour. A static, ‘differential refraction’ applied in a continuously variable way to explain these colours, is not an option.
This first example has the light going through the prism and the colours being observed, reflected on a surface. It is also possible to create the scam ‘rainbow spectrum’ by observing the colour bands directly through the prism. If you look at a bright window, through a prism sideways, you will notice the colour bands on either side of the window, along the line of refraction. Now we can see the reason for a concept like refraction, when we twist the prism back and forth and see the dramatic narrowing and broadening of the light image of the window. This measurable, apparently continuously variable phenomenon is the basis of concepts of refraction, and therefore of differential refraction, and it is this that allows us to produce a second version of Newton’s Scam Spectrum. If you twist the prism far enough, you reduce the light of the window to where the yellow part of the red band meets the blue band and – voila! – you have the ‘rainbow spectrum’, down the line of refraction.
But there are some problems here…. Except at extremes, when you broaden or shrink the window image, the colour bands remain unaltered to any visible extent. This at least suggests that they originate after the light is bent. They merely move and follow the light/dark contrast line. When brought together, both bands move towards the narrow angle of the prism, but the red one moves much more quickly and ‘catches up’ with the blue. They remain unaltered until reaching the scam spectrum, when they begin to overlap or intersect, with the yellow and blue stripes changing to green, until they merge and are replaced by one green stripe. Only now do the colour bands begin to shrink, but not equally. Orange and indigo stripes disappear first, with red, green and violet disappearing together as the light is choked off. (note: not one after the other as required by ‘different frequencies’)
Furthermore, the colour bands have the ability to move in two different directions, or at different speeds, within themselves. Let me explain. There is a small shelf edge projecting into the window view on the red band side, and this shows the identical red band as the side of the window, but much shorter and projected about one and a half band widths into the window, at the end of the shelf. Now as you tilt the prism to shrink the window, this shelf projection shrinks in accord with refraction, until about three colour band widths from the blue band, it disappears into the overall edge. But throughout this entire span, the small red band has been following the shrinking shelf, moving backwards into the main edge red band while the whole moves forward. The mathematics of ‘differential refraction’ cannot accommodate these different colour appearances, disappearances and movements.
Prisms certainly should be accorded much more honest, interested study. Another way of producing Newton’s Scam Spectrum requires a bit of set-up but is, I think, worth the interesting results.
Take flat black and flat white paint, mix equally to paint grey a pole 2 inches wide and 5 feet high. Paint a piece of cardboard 2×5 feet flat black and a piece 2×3 feet flat white (it’s relative dimensions and not actual measurements that matter). Stand the grey pole in front of the black board in bright light, and look at it through the prism sideways. You will see the clearest “rainbow spectrum” down the line of the pole. There are two ways of showing this to be a version of Newton’s Scam Spectrum. To do the first you put the white board over the lower half of the black, and look through the prism; suddenly at the white border the blue band turns to red and the red band to blue, continuing down the line of refraction. So we have the remarkable anachronism of Newton’s Scam Spectrum cheek to jowl in the same refractive context with a complete ‘inverted spectrum’, with red meeting violet in the middle! Placing the white just to the right or to the left of the pole produces an apparent ‘complete spectrum’ of either two red bands or two blue bands… clearly we are dealing with two separate colour bands capable of independent manipulation (always in relation to relative dark/light contrast), and not a rigid ‘differential refraction analyzing colours in a continuously variable way from a single unified beam of light’.
The trick to Newton’s Scam Spectrum in this case is the narrowness of the pole. Staple a sheet of writing paper to the pole and you will see the colour bands separated.
The spontaneous creation of colour in a prism is repeatedly seen to be more closely related to relative dark/light contrasts than to either refraction or any necessary red – blue continuum. The change of colour from blue to red down the line of refraction, merely because the background changes from relatively dark to relatively light, shows up as lies all the mathematically convenient concepts of prismatic colour production put forward by Newton and his idolizers. The fact that the blue band abuts the red one on the same line of refraction is also absolute proof that, far from being parts of a rightfully belonging together ‘rainbow spectrum’, the colour bands are indirectly related to each other at best. This shows (if previous evidence didn’t) the absurdity of there being any possibility of refraction, differential or otherwise, in the direct production of these phenomena of colour. Even the left-right orientation of the colour bands (usually red-relatively thicker part of prism, blue-relatively thinner when directly perceived; and the reverse when seen reflected on a surface) shows itself to be independent of the refractive angle when the dark/light contrast is reversed down the angle of refraction. The only immediately discernible refractive relationship is probably their width. There is every reason to note that the colours occur after the light is refracted in the context of relative bright/dark contrasts, and only in that sense ‘because’ of refraction.
Finally, and less explicitly, by twisting around a prism in sizeable bright light, the ‘rainbow spectrum’ can be artificially produced and projected onto surfaces, represented by at least three examples. One duplicates the window method, with the colour bands separated by a bright spot that is reduced by twisting the prism until the bands produce the made up ‘spectrum’. Another has the colour bands separated by a bright spot visible on a card near the prism, but reducing in size until 8-10 feet away (in this example) the colour bands intersect or overlap and a ‘spectrum’ appears. The third projected scam spectrum traces back to the ninety degree angle of the prism, but shows no bright spot. The colour bands are aligned on either side of the right angle and this is certainly a projective version of the narrow pole effect.
These are the few methods I have been able to attempt, and clumsily but definitively record; these could be structured with more precise measurements, and I’m sure there are other ways to artificially produce the row of colours. Again, every ‘rainbow colour spectrum’ seen associated with a prism can be resolved into the actually existing, separately and spontaneously arising, red band and blue band. These arise at opposite sides of bigger or smaller bodies of light, adjacent to relative darkness. The light involved in the red side of Newton’s Scam Spectrum is not involved in the creation of the blue side, and green is only produced through prisms by combining the pre-existing coloured light bands.
Furthermore…
It should be noted that the ‘inverted spectrum’ compresses to produce a magenta (or ‘red-purple’) stripe that replaces the red and violet stripes, exactly as the otherwise non-existent green replaces the blue and yellow stripes. Any physics of prismatic colour relationships, that is not fantasy, will have to address pairs of spontaneous colours occurring in two separate contexts, plus four apparently derived from their combining. The dogma of a prismatic, continuously variable ‘seven colours of the rainbow spectrum’, with everything derived from it, have been prejudicially made up by a cult of personalities for mathematical convenience and easy, suggestive salesmanship, and do not represent honest observation, let alone soundly reported investigative science.
HONEST OBSERVATION
The clear fact is that there can be no actual meaning to the incessantly proclaimed superiority of the ‘objective’ over the ‘subjective’. All human consciousness occurs either through the disappearance of any external stimulus into the human physiology, or through strictly internal stimulation…. Regardless, the actual perception is subjective, and the only meaningful discrimination is between the true and the false, in that the consciousness is related to its appropriate context. For example, ‘subjective’ and ‘objective’ are claimed to be scientific descriptions of the two contexts within which prismatic colour can be experienced. The honest observational report of these phenomena is that they are the ‘directly perceived’ and the ‘seen reflected’; that is, they are two visual contexts that cannot be proclaimed as one being superior to the other. They are each subjective experiences in different contexts. Supposedly ‘objective machines’ and ‘objective experiments’ are exclusively the product of, and assessed by, the subjective experiences and prejudices of their creators, and only hide this subjectivity behind a complex array of assumptions and manipulations that are anything but ‘objective’, and are merely proclaimed to be.
The first issue in considering light and colour is a clear description of what humans are conscious of when these are perceived, expressed in living terms available to unprejudiced common sense. One way of doing this is to note the indisputable fact that the light and colour we are conscious of cannot be the light and colour that disappears into the stimulation of the physical sense. That what is presented to consciousness is independent of external physicality is also shown by the light and colour hazily perceived in dreams, or intensified into visions and hallucinations. The only difference between ‘awake’ and ‘asleep’ perceptions, especially when the dream consciousness is intensified into visions and hallucinations, is that externally stimulated light and colour show experiences that are closely correlated with physical laws, while dreams and visions show no such necessity. It is clear that it is the form of stimulation that differs, not the inherent character of the light and colour consciously perceived. These facts have been dishonestly exploited by ‘Newtonians’ to proclaim any colours not in accord with their scam spectrum, as well as the discordant abrupt colour transitions and gaps, to be subjective – purely physiological and imaginary. The dual nature of what everyone is limited to being conscious of (including ‘strictly objective scientists’) shows no inherent need for the light and colour actually perceived to be themselves physical, or else they would have to obey physical laws throughout. Likewise, what the human self is, who is actually conscious of light and colour, is a ‘ghost in the machine’ directly inaccessible to mechanical materialism, although directly accessible to every self-conscious human.
It’s also crucial to keep in mind the difference between arithmetic, geometry and kinematics (theoretical or pure math) and mechanics and other applied math. Similar to the consciousness of light and colour, the realm of pure mathematics does not need to correspond to physical laws. Numbers do not physically exist, but can be applied to anything and everything. There are no physical phenomena that are exactly mathematical triangles or circles, etc. One and two dimensional mathematical realities, readily accessible to conscious manipulation, cannot embrace or represent physicality… (the examples are myriad). Like dreams and visions, pure mathematics may or may not be applicable to physical reality, and only gains external meaning when integrated into externally experienced and measured facts. There is no inherent need for pure math itself to be physical. The chaos brought about by the dogma that only mathematics provides a reliable reality, so that it is not necessary to carefully discriminate between the absolutely separate forms of pure and applied math, is basically the content of theoretically ‘proven’ mechanical materialism, including most of light theory. And of course, it is the ‘ghost in the machine’ who is doing all this math.
As many points of view as possible must be brought to bear on any light-form or mathematical-form seemingly related to our topic, in order that the physical/non-physical boundary be clearly respected.
PRISMATIC COLOUR
The following listing of pertinent observations is based on the prism being held sideways, with the refractive angle vertical. The light source has been the sun through double pane window glass using a 90 degree glass prism. It is not presented in any particular order. This is only a preliminary review, and I encourage everyone to get a prism and search through the many interesting and informative colour details, both directly perceived and seen reflected, and under many different conditions of light, shape, angle and intensity of contrast. It is fairly obvious where the sophisticated equipment of an optics lab could add precise measurements of changing widths, different speeds, angular occurrences, degree of contrast, etc.
1) Four colours (red and yellow; blue and violet) self-evidently spontaneously arise independently, apparently always in opposition, as repeatedly described above and with a few additional occurrences mentioned below.
2) Four colours arise apparently through combination, with orange or indigo occurring in a stable way between the red/yellow or the blue/violet and showing no tendency to expand or replace the spontaneous colours. The other two colours, green and magenta, are patently dynamic, occurring only when the yellow/blue or red/violet stripes move together – furthermore replacing these. When these have been replaced, the red-green-violet and the yellow-magenta-blue patterns remain stable in basic pattern (but not immutable), moving as units across the field of the prism until they are choked off or blurred out together at the edges (note- not one after the other).
3) Two brighter colours, yellow and blue, combine to produce the darker green, while on the other hand two darker colours, red and violet, combine to produce the brighter magenta. The former is only produced from the ‘rainbow spectrum’, the latter from the ‘inverted spectrum’.
4) The purely relative nature of the appearances. No matter whether brilliant white against dark black, or merely darker and brighter grey, the bands appear the same, merely brighter or darker. And if the relative positions of the darker/brighter interface are reversed, so are the colour bands regardless of the angle of refraction.
5) The ‘disappearing’ central body of light. Where does that ‘go’? It certainly doesn’t noticeably brighten the colours.
6) A rod or slot in a card placed to about up a 15 degree angle from horizontal shows no colour edge, while moved to about 20-25 degrees shows definite edge-effect colour bands. On the other hand, a circular dark object in bright light shows colour bands almost to the 90 degree poles, with the colour bands shrinking in width around the top and bottom.
7) The different movements of the colour bands as they are brought together need to be measured against the prism angles they are moving through, particularly the ‘retreating’ edge moving into a larger field because of slower speed. In general, both contexts of viewing show the red band to be more mobile than the blue band, despite reversed relationship to prism thickness.
8) When directly perceived, the red band can be seen to be shone through completely from behind, but the blue band has the violet stripe clearly in front of darkness, with the indigo at the darkness edge and only the blue clearly shone through from behind. Violet over darkness is easily shown in the directly perceived case, by a wooden rod against a bright sky – the wood pattern is visible through the violet; and in the seen reflected case by inserting a rod into the side of the blue band – it is not noticeable behind the violet stripe. As against this, the degree to which, and how, the dark edge is projected in front of the light to produce red needs to be carefully documented and considered. This is also required to grasp the significance of the reversal of the prism-angle/colour generation when the colours are directly perceived compared to being seen reflected on a surface.
Because of this relationship of the colour bands to the way the refracted light is bent, the ‘red band’ is more properly called the ‘dark refracted into a light field band’, or light band; and a ‘light refracted into a dark field band’, or dark band for the blue band.
9) For a couple of centuries it has been known that projecting a dark stripe in a bright field through the prism produces a reflected version of the ‘inverted spectrum’ shown by the directly perceived grey pole effect noted above. In fact I use their term, as it can only be properly called ‘reversed colour bands’, obviously caused by the comparative reversal of the dark/light interface.
10) The ‘rainbow spectrum’ produced by a prism is clearly not the result of continuous variation across a unified field. The sharp breaks between the colours, as well as the colours resulting from the combining of pre-existing colours and occurring in ‘non-spectrum’ contexts, need to be studied as basic qualities; they are not, like the scam spectrum, demonstrable illusions but are only proclaimed to be as they don’t fit the inadequate, continuously variable spectrum fantasy. The scam spectrum is at most a convenient way of studying aspects of the colour bands in proximity. The claim that this made-up row of colours sheds irrefutable light on all other forms of spontaneous colour generation is scientifically incompetent, and winds up being supported by circular argument or ‘authoritative dismissal’ of disagreeable facts. All colour phenomena need to be carefully described and studied in their own contexts before any interrelations can be considered.
The phenomena of colours occurring in relation to prisms have certainly not been carefully described and studied in their own context, as “one that shall a little consider it” soon discovers. Further observations appear to become more complex and lead to the limits where the colours can be directly related to the prism. Two things need to be re-stated and carried clearly in mind through all observations and considerations. One is that perceived light and perceived pure mathematics have no inherent need to relate to the physical – indeed, with mathematics the physical impossibility is as basic as the quite correct mathematical fact the one thing can equal another. In physical reality, one thing can only ‘equal’ another if certain facts and contexts are ignored or not noticed. Light is famous as a producer, or instrument, of illusions; so, again, as many points of view as possible must be brought to bear on any light-form or mathematical-form seemingly related to our topic, in order that the physical/non-physical boundary be clearly respected.
The second thing is that straightforward observations and considerations, that can be readily tested by anyone, need to ground initial description and study. So far this work has attempted not to go past observations that would have been available to rich people in 1700, and more broadly available since. It is this fact plus the obvious failure to find any actual undeniably spontaneous ‘spectrum’, that shows the scientific inadequacy of Newton’s suggestive enthusiasm; and the lack of even tentative due-diligence as to the validity of original claims (objectors have been merely attacked, not confronted with repeatable, in context observations such as given here) reveals the cult of personalities that has laid claim to this field. Their chaos of truth mixed with lies and misapprehensions has been made difficult to untangle.
To continue the listing:
11) The grey pole effect also occurs in a seen reflected version, if a grey strip is used on the face of the prism. I have used a 4-5mm wide strip of clear tape; the aim is to use a width that gives a full ‘inverted spectrum’. Then, blacking out various parts of the bright sides duplicates exactly the grey pole colour phenomena described previously as directly perceived (subjective), only in a seen reflected form (objective). This includes the scam spectrum directly adjacent to the ‘inverted spectrum’, down the line of refraction.
12) When perceived directly, the colour bands maintain an essentially uniform focus and configuration as the prism is moved farther away from the eye. Whereas, in the seen reflected bands the colours, patterns and focus change as the prism approaches the reflective surface, until about 5cm. from it (in this example) the colours have faded to obscurity.
13) Directly perceived, colours do not arise when the light is blocked by a rod or a slit in a card when placed between the eye and the prism, at any arm-length distance. Colours do arise from the light going to be reflected, when it is blocked after it leaves the prism and before the reflective surface. This fact of post-prism colour generation seems to be only observed by using the reflected colour pattern that has the colours on either side of a wide white centre (bright spots tested, that show no colours, do not show colours from the blocked light). It occurs both with the ‘rainbow spectrum’ (slot cut in card), or with the ‘inverted spectrum’ (using a rod). These are placed against the prism as the light leaves it, and moved towards the reflective surface. Both these methods show bright colours reflected when near the prism, with them fading until about 50cm from the prism (in this example) they are hardly noticeable.
14) It is significant that the plane-surface prisms give strong, varied colour patterns, while curve-surface prisms (lenses) produce faint, fuzzy colours, if at all. The clearest colour patterns I have so far noticed for lenses occurs by using a rod after the light has left the lens. This shows faint, fuzzy colour edges from about 8cm before the focal point to the same after. Despite clear refractive similarities, the curvature appears to at least approach one limit of prismatic colour.
15) When a grid of rods (I used four) is placed in the directly perceived context, and the prism twisted to compress the colour bands, a stable colour array of blue/magenta/green/m/g/m/g/m/g/yellow is produced. This remains stable until edges are approached, and occurs in both visual contexts with colour reversed.
16) There is no doubt that chemical effects are associated with the violet and heat effects with the red. How they disappear or integrate together into magenta is hard to imagine and needs to be traced with appropriate instruments and chemical tests.
THE TWO VISUAL CONTEXTS
Similarities
Relationships that remain consistent between both visual contexts, (i.e. directly perceived and seen reflected prism colours) include:
a) colours initiate at around 15 degree angle from square to the line of refraction.
b) the relationship that gives the two ‘spectrums’; i.e. the ‘rainbow spectrum’ always results from a bright centre with dark edges, and the ‘inverted spectrum’ from a dark centre with bright edges.
c) the violet stripe can be shown to occur over darkness, with the blue stripe and the entire red band, shone through from behind.
d) both perspectives are subject to the re-bending of the light as it leaves the prism. e) the relationship that gives green is always the ‘rainbow spectrum’, with magenta from the ‘inverse spectrum’.
f) I have not even tried to estimate the degree of light/dark contrast required to initiate the spontaneous colours – it would be dramatic if it were not basically the same for both perspectives. The fact that only one strip of transparent tape initiates colour effects shows that no great degree of contrast is required. On the other hand, abruptness of contrast and overall illumination of the field do seem involved.
Except for the left-right colour reversals involved, other similarities are:
the stable red-green-violet and blue-magenta-yellow patterns;
the stable magenta-green grid pattern;
the greater mobility of the red band;
the 15-20 degree initiation of colour along a rod and the bands’ ‘surrounding’ a circular object;
the entire range of grey pole effects.
the inability to expand the orange or indigo stripes except as all stripes expand and blur at extreme angles in some contexts.
Using both visual contexts allow for manipulations and preconditions that produce the following incomplete list of rows of colours:
Rainbow
Reversed rainbow
Inverse rainbow
Reversed inverse rainbow
Red-green-violet
Blue-magenta-yellow
Multiple magenta-green
Red band-red band
Blue band-blue band
Differences
The classic difference, noticed by everyone, is the reversal of the colours in their relationship to the thickness of the prism
Another difference is the production of the colour bands after the light has left the prism – it occurs with the seen reflected context but not with the directly perceived context.
It should be noted that the colour bands, when the rod is placed after the prism, are strong close to the prism; while the colour bands arising when the rod is placed before the prism and directly perceived are weakest close to the prism. The seen reflected colours also change more with prism twisting, than shown by the directly seen patterns,
The focus and configuration of the bands change when the prism is moved towards or away from the reflective surface, but not the eye.
The differences in transmitted light intensity (strong-seen reflected/weak-directly perceived) seem to be considered insignificant, but I’ve yet to see it explored.
LIMITS
The fact that the colours only spontaneously arise as edge or contrast effects shows that their occurrence is limited to a relationship or interaction at interfaces between relative light and dark. And that this relationship or interaction is also limited to the light/dark contrast being subject to refractive bending is shown by the fact that if the light is reflected internally in the prism so that the angle is reversed on exiting, no edge colours appear.
The light/dark contrast need not be absolute, but where provable unilluminated darkness occurs, the indigo band is directly perceived at the contrast line and the violet colour can be seen as illumination in front of the absolute darkness. For the same phenomenon to be occurring on the red side requires that the absolute darkness is bent in front of the illuminated side to give red colour, with the orange stripe being at the projected light/dark contrast line. These relationships also show how the reversal of directly perceived compared to seen reflected colour occurs, for if on the violet side the brightness precedes the darkness to the reflective surface, then the reflected brightness is seen through the following darkness to give red. The preceding darkness on the directly perceived red side strikes the reflective surface first to be seen behind the following darkness to give violet
The colour of each of the contrast effect bands must be only an interaction of brightness and darkness after it leaves the prism or colours would be the same in both contexts. It is the reversal of this dark/light interaction that produces the colour reversals that are evident. Further, the reversal requires that the darkness must be diverted as well as the light, and this shows that the colours generate in the same way in both contexts.
Simply put, it is a light/dark relationship that exits the prism, not colour.
The blue band, directly perceived, has the brightness diverted in front of the darker ground to give the blue band, with the same side having the brightness striking the reflective surface before the darkness, so that the brightness is seen through the following darkness to give the red band when seen or recorded reflected. On the red side directly perceived, the darkness is diverted in front of, and so seen through to the brightness to give the red band, with the seen reflected context having the darkness striking the reflective surface first and so seen through the following brightness to give the blue band. These are the initial limits to the occurrence of prismatic colour.
The fact that already coloured lights interact with one another makes the occurrence of green and magenta likely a limit of prismatic colour, especially as these can be seen to occur with the bringing together of the spontaneous coloured stripes – in both visual contexts. On the other hand, once complete the green and magenta stripes behave along with the remaining spontaneous colours, including forms of disappearance. The occurrence of indigo and orange, appearing spontaneously but not nearly as definitely as the other colours, is not so clearly the result of combination, and needs to be more precisely observed.
Some other limits to the production of prismatic colour are straightforward, some not so:
–Colours require a relatively slight, relatively abrupt contrast between brighter and darker fields in the refracted context. Below this no hint of colour occurs.
–The colours do not occur at right angles to the line of refraction up to about 20 degrees above this, after which they occur throughout the 70 degrees up to the line of refraction.
–The curvature of the prism faces is definitely a limiting factor.
–The entire phenomena in 13) indicates a limit of colour relationship or influence, if not actual production.
–The width limits of the colour bands could well be related to the specific refractive index and angle of each prism, and needs to be mathematically described in each case. The width limits do spread and become indistinct as the bright-dark transition is less abrupt.
It is necessary to consider and measure at least these limits, similarities and differences to gain a real, recordable, and repeatable picture.