On Monday, on a lark, we posted what we thought was The Shortest-Known Paper Published in a Serious Math Journal. Two succinct sentences.
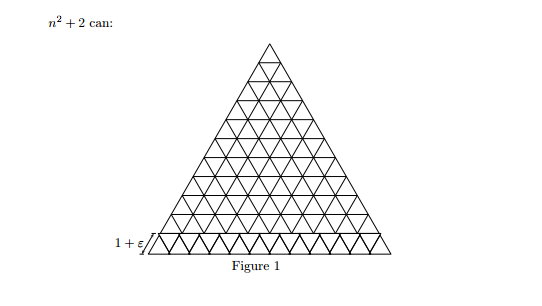
But then today, an OC reader gave us a heads-up on a more extreme display of brevity. In 2004, John Conway and Alexander Soifer, both working on mathematics at Princeton University, submitted to the American Mathematical Monthly what they believed was “a new world record in the number of words in a [math] paper.”
Soifer explains: “On April 28, 2004 … I submitted our paper that included just two words, ‘n2 + 2 can’ and our two drawings. [See one of them above.]” The story then continues: “The American Mathematical Monthly was surprised, and did not know what to do about our new world record of a 2‑word article. Two days later, on April 30, 2004, the Editorial Assistant Mrs. Margaret Combs acknowledged the receipt of the paper”:
The Monthly publishes exposition of mathematics at many levels, and it contains articles both long and short. Your article, however, is a bit too short to be a good Monthly article… A line or two of explanation would really help.
Soifer writers: “The same day at the coffee hour I asked John [Conway], ‘What do you think?’ His answer was concise, ‘Do not give up too easily.’ Accordingly, I replied [to] The Monthly the same day”:
I respectfully disagree that a short paper in general—and this paper in particular—merely due to its size must be “a bit too short to be a good Monthly article.” Is there a connection between quantity and quality?… We have posed a fine (in our opinion) open problem and reported two distinct “behold-style” proofs of our advance on this problem. What else is there to explain?
Soifer adds: “The Monthly, apparently felt outgunned, for on May 4, 2004, the reply came from The Monthly’s top gun, Editor-in-Chief Bruce Palka”:
The Monthly publishes two types of papers: “articles,” which are substantive expository papers ranging in length from about six to twenty-five pages, and “notes,” which are shorter, frequently somewhat more technical pieces (typically in the one-to-five page range). I can send your paper to the notes editor if you wish, but I expect that he’ll not be interested in it either because of its length and lack of any substantial accompanying text. The standard way in which we use such short papers these days is as “boxed filler” on pages that would otherwise contain a lot of the blank space that publishers abhor. If you’d allow us to use your paper in that way, I’d be happy to publish it.
Soifer concludes: “John Conway and I accepted the ‘filler’, and in the January 2005 issue our paper was published.” Victory!
Get more of the backstory here.
Related Content:
The Shortest-Known Paper Published in a Serious Math Journal: Two Succinct Sentences
The Math in Good Will Hunting is Easy: How Do You Like Them Apples?
It may be helpful to note that the title of the paper was “Can $n^2 + 1$ unit equilateral triangles cover an equilateral triangle of side $>n$, say $n+\varepsilon$?
Nah. That didn’t help me.
@Ed (and anyone else who’s confused) — it’s simple. If you divide an equilateral triangle of side n into equilateral triangles of side 1, you will get n^2 such triangles. (Look at all rows in the figure except the last, which has overlaps and two extra triangles). So if your big triangle’s side is a little bigger than n, you cannot cover it with n^2 triangles. They show, however, that you can cover it with n^2+2 triangles, by adding two triangles to the last row and doing this overlapping trick. The title asks (and the paper doesn’t answer): can you do it with n^2+1 triangles?
And according to the linked article by Soifer, the AMM editors pushed the authors’ title (comment #1 above) into the body of the paper and put in their own title instead. So the paper was a bit longer than two words.
Also, there’s that picture, which, though perhaps not worth a thousand words, would probably need at least a couple hundred words to describe clearly. And there was another picture with an alternative covering.
Thought-provoking piece . I was enlightened by the information — Does someone know where my assistant could grab a sample a form example to fill in ?
Does anyone else think that possibly, just POSSIBLY, the MAIN reason this got published more-or-less as submitted, was because JOHN CONWAY was involved? Just curious–I know nothing about the topic (go ahead, pile right on me, lol).